Some coupled fixed point theorems in quasi-partial metric spaces

Abstract

In this paper, we study some coupled fixed point results in a quasi-partial metric space. Also, we introduce some examples to support the useability of our results.

MSC:47H10, 54H25.

1 Introduction and preliminaries

In 1994, Matthews [1] introduced the notion of partial metric spaces and extended the Banach contraction principle from metric spaces to partial metric spaces. After that, many fixed point theorems in partial metric spaces have been given by several authors (for example, see [2–29]). Very recently, Haghi et al. [30, 31] showed in their interesting paper that some of fixed point theorems in partial metric spaces can be obtained from metric spaces.

Following Matthews [1], the notion of partial metric space is given as follows.

Definition 1.1 [1]

A partial metric on a nonempty set X is a function $p:X\times X\to {\mathbb{R}}^{+}$ such that for all $x,y,z\in X$:

(${\mathrm{p}}_1$) $x=y⟺p(x,x)=p(x,y)=p(y,y)$,

(${\mathrm{p}}_2$) $p(x,x)\le p(x,y)$,

(${\mathrm{p}}_3$) $p(x,y)=p(y,x)$,

(${\mathrm{p}}_4$) $p(x,y)\le p(x,z)+p(z,y)-p(z,z)$.

A partial metric space is a pair $(X,p)$ such that X is a nonempty set and p is a partial metric on X.

Karapinar et al. [32] introduced the concept of quasi-partial metric spaces and studied some fixed point theorems on quasi-partial metric spaces.

Definition 1.2 [32]

A quasi-partial metric on a nonempty set X is a function $q:X\times X\to {\mathbb{R}}^{+}$ which satisfies:

(${\mathrm{QPM}}_1$) If $q(x,x)=q(x,y)=q(y,y)$, then $x=y$,

(${\mathrm{QPM}}_2$) $q(x,x)\le q(x,y)$,

(${\mathrm{QPM}}_3$) $q(x,x)\le q(y,x)$, and

(${\mathrm{QPM}}_4$) $q(x,y)+q(z,z)\le q(x,z)+q(z,y)$

for all $x,y,z\in X$.

A quasi-partial metric space is a pair $(X,q)$ such that X is a nonempty set and q is a quasi-partial metric on X.

Let q be a quasi-partial metric space on the set X. Then

$$d_q(x,y)=q(x,y)+q(y,x)-p(x,x)-p(y,y)$$

is a metric on X.

Definition 1.3 [32]

Let $(X,q)$ be a quasi-partial metric space. Then:

• (1) A sequence $(x_n)$ converges to a point $x\in X$ if and only if

  $$q(x,x)=\underset{n\to \mathrm{\infty }}{lim}q(x,x_n)=\underset{n\to \mathrm{\infty }}{lim}q(x_n,x).$$

• (2) A sequence $(x_n)$ is called a Cauchy sequence if ${lim}_{n,m\to \mathrm{\infty }}p(x_n,x_m)$ and ${lim}_{n,m\to \mathrm{\infty }}p(x_n,x_m)$ exist (and are finite).

• (3) The quasi-partial metric space $(X,q)$ is said to be complete if every Cauchy sequence $(x_n)$ in X converges, with respect to ${\tau }_q$, to a point $x\in X$ such that

  $$q(x,x)=\underset{n,m\to \mathrm{\infty }}{lim}q(x_n,x_m)=\underset{n,m\to \mathrm{\infty }}{lim}q(x_m,x_n).$$

The following lemma is crucial in our work.

Lemma 1.1 [32]

Let $(X,q)$ be a quasi-partial metric space. Then the following statements hold true:

• (A) If $q(x,y)=0$, then $x=y$.

• (B) If $x\ne y$, then $q(x,y)>0$ and $q(y,x)>0$.

Bhaskar and Lakshmikantham [33] introduced the concept of coupled fixed point and studied some nice coupled fixed point theorems. Later, Lakshmikantham and Ćirić [34] introduced the notion of a coupled coincidence point of mappings. For some works on a coupled fixed point, we refer the reader to [35–46].

Definition 1.4 [33]

Let X be a nonempty set. We call an element $(x,y)\in X\times X$ a coupled fixed point of the mapping $F:X\times X\to X$ if

$$F(x,y)=x\text{and}F(y,x)=y.$$

Definition 1.5 [34]

An element $(x,y)\in X\times X$ is called a coupled coincidence point of the mappings $F:X\times X\to X$ and $g:X\to X$ if

$$F(x,y)=gx\text{and}F(y,x)=gy.$$

Abbas et al. [47] introduced the concept of w-compatible mappings as follows.

Definition 1.6 [47]

Let X be a nonempty set. We say that the mappings $F:X\times X\to X$ and $g:X\to X$ are w-compatible if $gF(x,y)=F(gx,gy)$ whenever $gx=F(x,y)$ and $gy=F(y,x)$.

In this paper, we study some coupled fixed point theorems in the setting of quasi-partial metric spaces. We introduce some examples to support our results.

2 The main results

We start this section with the following coupled fixed point theorem.

Theorem 2.1 Let $(X,q)$ be a quasi-partial metric space, $g:X\to X$ and $F:X\times X\to X$ be two mappings. Suppose that there exist $k_1$, $k_2$ and $k_3$ in $[0,1)$ with $k_1+k_2+k_3<1$ such that the condition

$$\begin{array}{r}q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\\ \le k_1(q(gx,g{x}^{\ast })+q(gy,g{y}^{\ast }))+k_2(q(gx,F(x,y))+q(gy,F(y,x)))\\ +k_3(q(g{x}^{\ast },F(x^{\ast },y^{\ast }))+q(g{y}^{\ast },F(y^{\ast },x^{\ast })))\end{array}$$

(2.1)

holds for all $x,y,x^{\ast },y^{\ast }\in X$. Also, suppose the following hypotheses:

• (1) $F(X\times X)\subseteq gX$.

• (2) $g(X)$ is a complete subspace of X with respect to the quasi-partial metric q.

Then the mappings F and g have a coupled coincidence point $(u,v)$ satisfying $gu=F(u,v)=F(v,u)=gu$.

Moreover, if F and g are w-compatible, then F and g have a unique common fixed point of the form $(u,u)$.

Proof Let $x_0,y_0\in X$. Since $F(X\times X)\subseteq gX$, we put $g{x}_1=F(x_0,y_0)$ and $g{y}_1=F(y_0,x_0)$. Again, since $F(X\times X)\subseteq gX$, we put $g{x}_2=F(x_1,y_1)$ and $g{y}_2=F(y_1,x_1)$. Continuing this process, we can construct two sequences $(g{x}_n)$ and $(g{y}_n)$ in X such that

$$g{x}_n=F(x_{n-1},y_{n-1}),\mathrm{\forall }n\in \mathbb{N},$$

and

$$g{y}_n=F(y_{n-1},x_{n-1}),\mathrm{\forall }n\in \mathbb{N}.$$

• Let $n\in \mathbb{N}$. Then by inequality (2.1), we obtain

  

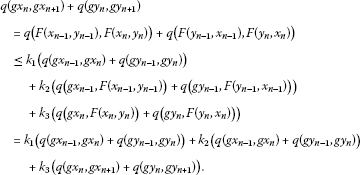  (2.2)

From (2.2), we have

$$q(g{x}_n,g{x}_{n+1})+q(g{y}_n,g{y}_{n+1})\le \frac{k_1+k_2}{1-k_3}(q(g{x}_{n-1},g{x}_n)+q(g{y}_{n-1},g{y}_n)).$$

(2.3)

Put $k=\frac{k_1+k_2}{1-k_3}$. Then $k<1$. Repeating (2.3) n-times, we get

$$q(g{x}_n,g{x}_{n+1})+q(g{y}_n,g{y}_{n+1})\le k^n(q(g{x}_0,g{x}_1)+q(g{y}_0,g{y}_1)).$$

Let m and n be natural numbers with $m>n$. Then

$$\begin{array}{rl}q(g{x}_n,g{x}_m)+q(g{y}_n,g{y}_m)& \le \sum _{i=n}^{m-1}q(g{x}_i,g{x}_{i+1})+q(g{y}_i,g{y}_{i+1})\\ \le \sum _{i=n}^{m-1}{k}^i(q(g{x}_0,g{x}_1)+q(g{y}_0,g{y}_1))\\ \le \frac{k^n}{1-k}(q(g{x}_0,g{x}_1)+q(g{y}_0,g{y}_1)).\end{array}$$

(2.4)

Letting $n,m\to +\mathrm{\infty }$, we get

$$\underset{n,m\to +\mathrm{\infty }}{lim}q(g{x}_n,g{x}_m)=\underset{n,m\to +\mathrm{\infty }}{lim}q(g{y}_n,g{y}_m)=0.$$

(2.5)

• By similar arguments as above, we can show that

  $$\underset{n,m\to +\mathrm{\infty }}{lim}q(g{x}_m,g{x}_n)=\underset{n,m\to +\mathrm{\infty }}{lim}q(g{y}_m,g{y}_n)=0.$$

  (2.6)

Thus the sequences $(g{x}_n)$ and $(g{y}_n)$ are Cauchy in $(gX,q)$. Since $(gX,q)$ is complete, there are u and v in X such that $g{x}_n\to gu$ and $g{y}_n\to gy$ with respect to ${\tau }_q$, that is,

$$\begin{array}{rcl}q(gu,gu)& =& \underset{n\to +\mathrm{\infty }}{lim}q(gu,g{x}_n)=\underset{n\to +\mathrm{\infty }}{lim}q(g{x}_n,gu)\\ =& \underset{n,m\to +\mathrm{\infty }}{lim}q(g{x}_m,g{x}_n)=\underset{n,m\to +\mathrm{\infty }}{lim}q(g{x}_n,g{x}_m)\end{array}$$

and

$$\begin{array}{rcl}q(gv,gv)& =& \underset{n\to +\mathrm{\infty }}{lim}q(gv,g{y}_n)=\underset{n\to +\mathrm{\infty }}{lim}q(g{y}_n,gv)\\ =& \underset{n,m\to +\mathrm{\infty }}{lim}q(g{y}_m,g{y}_n)=\underset{n,m\to +\mathrm{\infty }}{lim}q(g{y}_n,g{y}_m).\end{array}$$

From (2.5) and (2.6), we have

$$\begin{array}{rl}q(gu,gu)& =\underset{n\to +\mathrm{\infty }}{lim}q(gu,g{x}_n)=\underset{n\to +\mathrm{\infty }}{lim}q(g{x}_n,gu)\\ =\underset{n,m\to +\mathrm{\infty }}{lim}q(g{x}_m,g{x}_n)=\underset{n,m\to +\mathrm{\infty }}{lim}q(g{x}_n,g{x}_m)=0\end{array}$$

(2.7)

and

$$\begin{array}{rl}q(gv,gv)& =\underset{n\to +\mathrm{\infty }}{lim}q(gv,g{y}_n)=\underset{n\to +\mathrm{\infty }}{lim}q(g{y}_n,gv)\\ =\underset{n,m\to +\mathrm{\infty }}{lim}q(g{y}_m,g{y}_n)=\underset{n,m\to +\mathrm{\infty }}{lim}q(g{y}_n,g{y}_m)=0.\end{array}$$

(2.8)

For n in ℕ, we obtain

$$\begin{array}{rcl}q(g{x}_{n+1},F(u,v))& \le & q(g{x}_{n+1},gu)+q(gu,F(u,v))-q(gu,gu)\\ \le & q(g{x}_{n+1},gu)+q(gu,F(u,v))\\ \le & q(g{x}_{n+1},gu)+q(gu,g{x}_{n+1})+q(g{x}_{n+1},F(u,v))-q(g{x}_{n+1},g{x}_{n+1})\\ \le & q(g{x}_{n+1},gu)+q(gu,g{x}_{n+1})+q(g{x}_{n+1},F(u,v)).\end{array}$$

On letting $n\to +\mathrm{\infty }$ in the above inequalities and using (2.7) and (2.8), we have

$$\underset{n\to +\mathrm{\infty }}{lim}q(g{x}_{n+1},F(u,v))=q(gu,F(u,v)).$$

(2.9)

Similarly, we have

$$\underset{n\to +\mathrm{\infty }}{lim}q(g{y}_{n+1},F(v,u))=q(gv,F(v,u)).$$

(2.10)

• We show that $gu=F(u,v)$ and $gv=F(v,u)$.

For $n\in \mathbb{N}$, we have

$$\begin{array}{c}q(g{x}_{n+1},F(u,v))+q(g{y}_{n+1},F(v,u))\hfill \\ =q(F(x_n,y_n),F(u,v))+q(F(y_n,x_n),F(v,u))\hfill \\ \le k_1(q(g{x}_n,gu)+q(g{y}_n,gv))+k_2(q(g{x}_n,F(x_n,y_n))+q(g{y}_n,F(y_n,x_n))\hfill \\ +k_3(q(gu,F(u,v))+q(gv,F(v,u)))\hfill \\ =k_1(q(g{x}_n,gu)+q(g{y}_n,gv))+k_1(q(g{x}_n,g{x}_{n+1}))+q(g{y}_n,g{y}_{n+1}))\hfill \\ +k_3(q(gu,F(u,v))+q(gv,F(v,u))).\hfill \end{array}$$

Letting $n\to +\mathrm{\infty }$ in above inequalities and using (2.9)-(2.10), we get

$$q(gu,F(u,v))+q(gv,F(v,u))\le k_3(q(gu,F(u,v))+q(gv,F(v,u))).$$

Since $k_3<1$, we get $q(gu,F(u,v))=q(gv,F(v,u))=0$. By Lemma 1.1, we get $gu=F(u,v)$ and $gv=F(v,u)$. Next, we will show that $gu=gv$. Now, from (2.1) we have

$$\begin{array}{c}q(gu,gv)+q(gv,gu)\hfill \\ =q(F(u,v),F(v,u))+q(F(v,u),F(u,v))\hfill \\ \le k_1(q(gu,gv)+q(gv,gu))+k_2(q(gu,F(u,v))+q(gv,F(v,u)))\hfill \\ +k_3(q(gv,F(v,u))+q(gu,F(u,v)))\hfill \\ =k_1(q(gu,gv)+q(gv,gu))+k_2(q(gu,gu)+q(gv,gv))+k_3(q(gv,gv)+q(gu,gu)).\hfill \end{array}$$

Using (2.7) and (2.8), we obtain

$$q(gu,gv)+q(gv,gu)\le k_1(q(gu,gv)+q(gv,gu)).$$

Since $k_1<1$, we have $q(gu,gv)=q(gv,gu)=0$ By Lemma 1.1, we get that $gu=gv$. Finally, assume that g and F are w-compatible. Let $u_1=gu$ and $v_1=gv$. Then

$$g{u}_1=ggu=g(F(u,v))=F(gu,gv)=F(u_1,v_1)$$

(2.11)

and

$$g{v}_1=ggv=g(F(v,u))=F(gv,gu)=F(v_1,u_1).$$

(2.12)

From (2.11) and (2.12), we can show that

$$q(g{u}_1,g{u}_1)=q(g{v}_1,g{v}_1).$$

• We claim that $g{u}_1=gu$ and $g{v}_1=gv$.

From (2.1), we have

$$\begin{array}{c}q(g{u}_1,gu)+q(g{v}_1,gv)\hfill \\ =q(F(u_1,v_1),F(u,v))+q(F(v_1,u_1),F(v,u))\hfill \\ \le k_1(q(g{u}_1,gu)+q(g{v}_1,gv))+k_2(q(g{u}_1,F(u_1,v_1))+q(g{v}_1,F(v_1,u_1)))\hfill \\ +k_3(q(gu,F(u,v))+q(gv,F(v,u)))\hfill \\ =k_1(q(g{u}_1,gu)+q(g{v}_1,gv))+k_2(q(g{u}_1,g{u}_1)+q(g{v}_1,g{v}_1))\hfill \\ +k_3(q(gu,gu)+q(gv,gv))\hfill \\ =k_1(q(g{u}_1,gu)+q(g{v}_1,gv)).\hfill \end{array}$$

Since $k_1<1$, we conclude that $q(g{u}_1,gu)=q(g{v}_1,gv)=0$. By Lemma 1.1, we get $g{u}_1=gu$ and $g{v}_1=gv$. Therefore $u_1=g{u}_1$ and $v_1=g{v}_1$. Again, since $gu=gv$, we get $u_1=v_1$. Hence F and g have a unique common coupled fixed point of the form $(u,u)$. □

Corollary 2.1 Let $(X,q)$ be a quasi-partial metric space, $g:X\to X$ and $F:X\times X\to X$ be two mappings. Suppose that there exist a, b, c, d, e, f in $[0,1)$ with $a+b+c+d+e+f<1$ such that

$$\begin{array}{r}q(F(x,y),F(x^{\ast },y^{\ast }))\\ \le aq(gx,g{x}^{\ast })+bq(gy,g{y}^{\ast })+cq(gx,F(x,y))+dq(gy,F(y,x))\\ +eq(g{x}^{\ast },F(x^{\ast },y^{\ast }))+fq(g{y}^{\ast },F(y^{\ast },x^{\ast }))\end{array}$$

(2.13)

holds for all $x,y,x^{\ast },y^{\ast }\in X$. Also, suppose the following hypotheses:

• (1) $F(X\times X)\subseteq gX$.

• (2) $g(X)$ is a complete subspace of X with respect to the quasi-partial metric q.

Then F and g have a coupled coincidence point $(u,v)$ satisfying $gu=F(u,v)=F(v,u)=gu$.

Moreover, if F and g are w-compatible, then F and g have a unique common fixed point of the form $(u,u)$.

Proof Given $x,y,x^{\ast },y^{\ast }\in X$. From (2.13), we have

$$\begin{array}{r}q(F(x,y),F(x^{\ast },y^{\ast }))\\ \le aq(gx,g{x}^{\ast })+bq(gy,g{y}^{\ast })+cq(gx,F(x,y))+dq(gy,F(y,x))\\ +eq(g{x}^{\ast },F(x^{\ast },y^{\ast }))+fq(g{y}^{\ast },F(y^{\ast },x^{\ast }))\end{array}$$

(2.14)

and

$$\begin{array}{r}q(F(y,x),F(y^{\ast },x^{\ast }))\\ \le aq(gy,g{y}^{\ast })+bq(gx,g{x}^{\ast })+cq(gy,F(y,x))+dq(gx,F(x,y))\\ +eq(g{y}^{\ast },F(y^{\ast },x^{\ast }))+fq(g{x}^{\ast },F(x^{\ast },y^{\ast })).\end{array}$$

(2.15)

Adding inequality (2.14) to inequality (2.15), we get

$$\begin{array}{r}q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\\ \le (a+b)(q(gx,g{x}^{\ast })+q(gy,g{y}^{\ast }))+(c+d)(q(gx,F(x,y))+q(gy,F(y,x)))\\ +(e+f)(q(g{x}^{\ast },F(x^{\ast },y^{\ast }))+q(g{y}^{\ast },F(y^{\ast },x^{\ast }))).\end{array}$$

Thus, the result follows from Theorem 2.1. □

Corollary 2.2 Let $(X,q)$ be a quasi-partial metric space, let $g:X\to X$ and $F:X\times X\to X$ be two mappings. Suppose that there exists $k\in [0,1)$ with $k_1+k_2+k_3<1$ such that

$$q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\le k(q(gx,g{x}^{\ast })+q(gy,g{y}^{\ast }))$$

holds for all $x,y,x^{\ast },y^{\ast }\in X$. Also, suppose the following hypotheses:

• (1) $F(X\times X)\subseteq gX$.

• (2) $g(X)$ is a complete subspace of X with respect to the quasi-partial metric q.

Then F and g have a coupled coincidence point $(u,v)$ satisfying $gu=F(u,v)=F(v,u)=gu$.

Moreover, if F and g are w-compatible, then F and g have a unique common fixed point of the form $(u,u)$.

Corollary 2.3 Let $(X,q)$ be a quasi-partial metric space, $g:X\times X$ and $F:X\times X\to X$ be two mappings. Suppose that there exists $k\in [0,1)$ with $k<1$ such that

$$q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\le k(q(gx,F(x,y))+q(gy,F(y,x)))$$

holds for all $x,y,x^{\ast },y^{\ast }\in X$. Also, suppose the following hypotheses:

• (1) $F(X\times X)\subseteq X$.

• (2) $g(X)$ is a complete subspace of X with respect to the quasi-partial metric q.

Then F and g have a coupled coincidence point $(u,v)$ satisfying $gu=F(u,v)=F(v,u)=gu$.

Moreover, if F and g are w-compatible, then F and g have a unique common fixed point of the form $(u,u)$.

Corollary 2.4 Let $(X,q)$ be a quasi-partial metric space, $g:X\to X$ and $F:X\times X\to X$ be two mappings. Suppose that there exists $k\in [0,1)$ with $k<1$ such that

$$q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\le k(q(g{x}^{\ast },F(x^{\ast },y^{\ast }))+q(g{y}^{\ast },F(y^{\ast },x^{\ast })))$$

holds for all $x,y,x^{\ast },y^{\ast }\in X$. Also, suppose the following hypotheses:

• (1) $F(X\times X)\subseteq gX$.

• (2) $g(X)$ is a complete subspace of X with respect to the quasi-partial metric q.

Then F and g have a coupled coincidence point $(u,v)$ satisfying $gu=F(u,v)=F(v,u)=gu$.

Moreover, if F and g are w-compatible, then F and g have a unique common fixed point of the form $(u,u)$.

Let $g=I_X$ (the identity mapping) in Theorem 2.2 and Corollaries 2.1-2.4. Then we have the following results.

Corollary 2.5 Let $(X,q)$ be a quasi-partial metric space and let $F:X\times X\to X$ be a mapping. Suppose that there exist $k_1,k_2,k_3\in [0,1)$ with $k_1+k_2+k_3<1$ such that

$$\begin{array}{r}q(F(x,y),F(x^{\ast },y^{\ast }))+g(F(y,x),F(y^{\ast },x^{\ast }))\\ \le k_1(q(x,x^{\ast })+q(y,y^{\ast }))+k_2(q(x,F(x,y))+q(y,F(y,x)))\\ +k_3(q(x^{\ast },F(x^{\ast },y^{\ast }))+q(y^{\ast },F(y^{\ast },x^{\ast })))\end{array}$$

holds for all $x,y,x^{\ast },y^{\ast }\in X$.

Then F has a unique coupled fixed point of the form $(u,u)$.

Corollary 2.6 Let $(X,q)$ be a quasi-partial metric space and let $F:X\times X\to X$ be a mapping. Suppose that there exist $a,b,c,d,e,f\in [0,1)$ with $a+b+c+d+e+f<1$ such that

$$\begin{array}{r}q(F(x,y),F(x^{\ast },y^{\ast }))\\ \le aq(x,x^{\ast })+bq(y,y^{\ast })+cq(x,F(x,y))+dq(y,F(y,x))\\ +eq(x^{\ast },F(x^{\ast },y^{\ast }))+fq(y^{\ast },F(y^{\ast },x^{\ast }))\end{array}$$

holds for all $x,y,x^{\ast },y^{\ast }\in X$.

Then F has a unique coupled fixed point of the form $(u,u)$.

Corollary 2.7 Let $(X,q)$ be a complete quasi-partial metric space and let $F:X\times X\to X$ be a mapping. Suppose that there exists $k\in [0,1)$ such that

$$q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\le k(q(x,x^{\ast })+q(y,y^{\ast }))$$

holds for all $x,y,x^{\ast },y^{\ast }\in X$.

Then F has a unique coupled fixed point of the form $(u,u)$.

Corollary 2.8 Let $(X,q)$ be a complete quasi-partial metric space and let $F:X\times X\to X$ be a mapping. Suppose that there exists $k\in [0,1)$ with $k<1$ such that

$$q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\le k(q(x,F(x,y))+q(y,F(y,x)))$$

holds for all $x,y,x^{\ast },y^{\ast }\in X$.

Then F has a unique coupled fixed point of the form $(u,u)$.

Corollary 2.9 Let $(X,q)$ be a complete quasi-partial metric space and let $F:X\times X\to X$ be a mapping. Suppose that there exists $k\in [0,1)$ with $k<1$ such that

$$q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\le k(q(x^{\ast },F(x^{\ast },y^{\ast }))+q(y^{\ast },F(y^{\ast },x^{\ast })))$$

holds for all $x,y,x^{\ast },y^{\ast }\in X$.

Then F has a unique coupled fixed point of the form $(u,u)$.

Theorem 2.2 Let $(X,q)$ be a complete quasi-partial metric space and let $F:X\times X\to X$, $g:X\to X$ be two mappings. Suppose that there exists a function $\varphi :gX\to {\mathbb{R}}_{+}$ such that

$$q(gx,F(x,y))+q(gy,F(y,x))\le \varphi (gx)+\varphi (gy)-\varphi (F(x,y))-\varphi (F(y,x))$$

holds for all $(x,y)\in X\times X$. Also, assume that the following hypotheses are satisfied:

• (a) $F(X\times X)\subset gX$;

• (b) if $G:X\times X\to \mathbb{R}$, $G(x,y)=q(F(x,y),gx)$, then for each sequence $(g{x}_n,g{y}_n)\to (u,v)$, we have $G(u,v)\le k{lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}G(x_n,y_n)$ for some $k>0$.

Then F and g have a coupled coincidence point $(u,v)$. In addition, $q(gu,gu)=0$ and $q(gv,gv)=0$.

Proof Consider $(x_0,y_0)\in X\times X$. As $F(X\times X)\subset gX$, there are $x_1$ and $y_1$ from X such that $g{x}_1=F(x_0,y_0)$ and $g{y}_1=F(y_0,x_0)$. By repeating this process, we construct two sequences, $(x_n)$ and $(y_n)$ with $g{x}_{n+1}=F(x_n,y_n)$ and $g{y}_{n+1}=F(y_n,x_n)$.

The fourth property of the quasi-partial metric space gives us

$$\begin{array}{c}q(g{x}_n,g{x}_{n+2})+q(g{y}_n,g{y}_{n+2})\hfill \\ \le q(g{x}_n,g{x}_{n+1})+q(g{x}_{n+1},g{x}_{n+2})\hfill \\ -q(g{x}_{n+1},g{x}_{n+1})+q(g{y}_n,g{y}_{n+1})+q(g{y}_{n+1},g{y}_{n+2})-q(g{y}_{n+1},g{y}_{n+1})\hfill \\ \le q(g{x}_n,g{x}_{n+1})+q(g{x}_{n+1},g{x}_{n+2})+q(g{y}_n,g{y}_{n+1})+q(g{y}_{n+1},g{y}_{n+2}).\hfill \end{array}$$

Based on the above inequality, for $m>n$, we obtain

$$q(g{x}_n,g{x}_m)+q(g{y}_n,g{y}_m)\le \sum _{k=n}^{m-1}[q(g{x}_k,g{x}_{k+1})+q(g{y}_k,g{y}_{k+1})]$$

(2.16)

$$\begin{array}{rc}=& \sum _{k=n}^{m-1}[q(g{x}_k,F(x_k,y_k))+q(g{y}_k,F(y_k,x_k))]\\ \le & \sum _{k=n}^{m-1}[\varphi (g{x}_k)+\varphi (g{y}_k)-\varphi (F(x_k,y_k))-\varphi (F(y_k,x_k))]\\ =& \sum _{k=n}^{m-1}[\varphi (g{x}_k)+\varphi (g{y}_k)-\varphi (g{x}_{k+1})-\varphi (g{y}_{k+1})]\\ =& \varphi (g{x}_n)+\varphi (g{y}_n)-\varphi (g{x}_m)-\varphi (g{y}_m).\end{array}$$

(2.17)

Consider $S_n(x)={\sum }_{k=0}^n[q(g{x}_k,g{x}_{k+1})+q(g{y}_k,g{y}_{k+1})]$. Inequality (2.17) implies that

$$S_n(x)\le \varphi (g{x}_0)+\varphi (g{y}_0),$$

hence the nondecreasing sequence $\{S_n\}$ is bounded, so it is convergent. Taking the limit as $n,m\to +\mathrm{\infty }$ in (2.16), we conclude that

$$\underset{n,m\to +\mathrm{\infty }}{lim}q(g{x}_n,g{x}_m)=\underset{n,m\to +\mathrm{\infty }}{lim}q(g{y}_n,g{y}_m).$$

Using similar arguments, it can be proved that

$$\underset{n,m\to \mathrm{\infty }}{lim}q(g{x}_m,g{x}_n)=\underset{n,m\to \mathrm{\infty }}{lim}q(g{y}_m,g{y}_n)=0.$$

As $(g{x}_n)$ and $(g{y}_n)$ are Cauchy sequences in the complete quasi-partial metric space $(X,q)$, there are u, v in X such that $u={lim}_{n\to \mathrm{\infty }}g{x}_n$ and $v={lim}_{n\to \mathrm{\infty }}g{v}_n$. Having in mind hypothesis (b), the following relations hold true:

$$\begin{array}{rcl}0& \le & q(F(u,v),gu)=G(u,v)\le k\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}G(x_n,y_n)\\ =& k\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}q(F(x_n,y_n),g{x}_n)\\ =& k\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}q(g{x}_{n+1},g{x}_n)\\ =& 0.\end{array}$$

We get $q(F(u,v),gu)=0$, and by Lemma 1.1, it follows that $F(u,v)=g(u)$.

Analogously, it can be proved that $F(v,u)=gv$.

As a conclusion, we have obtained that $(u,v)$ is a coupled coincidence point of the mappings F and g, and $q(gu,gu)=0$, $q(gv,gv)=0$. □

Corollary 2.10 Let $(X,q)$ be a complete quasi-partial metric space and let $F:X\times X\to X$ be a mapping. Suppose that there exists a function $\varphi :X\to {\mathbb{R}}_{+}$ such that

$$q(x,F(x,y))+q(y,F(y,x))\le \varphi (x)+\varphi (y)-\varphi (F(x,y))-\varphi (F(y,x))$$

holds for all $(x,y)\in X\times X$. Also, assume that the following hypotheses are satisfied:

• (a) $F(X\times X)\subset X$;

• (b) if $G:X\times X\to \mathbb{R}$, $G(x,y)=q(F(x,y),x)$, then for each sequence $(x_n,y_n)\to (u,v)$, we have $G(u,v)\le k{lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}G(x_n,y_n)$ for some $k>0$.

Then F has a coupled coincidence point $(u,v)$. In addition, $q(u,u)=0$ and $q(v,v)=0$.

Proof Follows from Theorem 2.2 by taking $g=I_X$ (the identity mapping). □

3 Examples

Now, we introduce some examples to support our results.

Example 3.1 On the set $X=[0,1]$, define

$$q:X\times X\to {\mathbb{R}}^{+},q(x,y)=|x-y|+x.$$

Also, define

$$F:X\times X\to X,F(x,y)=\{\begin{array}{cc}\frac{1}{4}(x-y),\hfill & x\ge y;\hfill \\ 0,\hfill & x<y,\hfill \end{array}$$

and $g:X\to X$ by $gx=\frac{1}{2}x$. Then

• (1) $(X,q)$ is a complete quasi-partial metric space.

• (2) $F(X\times X)\subseteq gX$.

• (3) For any $x,y,x^{\ast },y^{\ast }\in X$, we have

  $$q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\le \frac{1}{2}(q(gx,g{x}^{\ast })+q(gy,g{y}^{\ast })).$$

Proof The proofs of (1) and (2) are clear. To prove (3), we consider the following cases.

Case 1: $x<y$ and $x^{\ast }<y^{\ast }$. Here we have

$$F(x,y)=0,F(x^{\ast },y^{\ast })=0,F(y,x)=\frac{y-x}{4},F(y^{\ast },x^{\ast })=\frac{y^{\ast }-x^{\ast }}{4}.$$

Therefore

$$\begin{array}{c}q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\hfill \\ =q(0,0)+q(\frac{x-y}{4},\frac{y^{\ast }-x^{\ast }}{4})\hfill \\ =\frac{1}{4}|(y-x)-(y^{\ast }-x^{\ast })|+\frac{1}{4}(y-x)\hfill \\ \le \frac{1}{2}|(\frac{1}{2}y-\frac{1}{2}x)-(\frac{1}{2}{y}^{\ast }-\frac{1}{2}{x}^{\ast })|+\frac{1}{2}(\frac{1}{2}y-\frac{1}{2}x)\hfill \\ \le \frac{1}{2}|(\frac{1}{2}{x}^{\ast }-\frac{1}{2}x)-(\frac{1}{2}{y}^{\ast }-\frac{1}{2}y)|+\frac{1}{2}(\frac{1}{2}y+\frac{1}{2}x)\hfill \\ \le \frac{1}{2}(|\frac{1}{2}{x}^{\ast }-\frac{1}{2}x|+\frac{1}{2}x+|\frac{1}{2}{y}^{\ast }-\frac{1}{2}y|+\frac{1}{2}y)\hfill \\ =\frac{1}{2}(|g{x}^{\ast }-gx|+gx+|gy-g{y}^{\ast }|+gy)\hfill \\ =\frac{1}{2}(q(gx,g{x}^{\ast })+q(gy,g{y}^{\ast })).\hfill \end{array}$$

Case 2: $x<y$ and $x^{\ast }\ge y^{\ast }$. Here we have

$$F(x,y)=0,F(x^{\ast },y^{\ast })=\frac{x^{\ast }-y^{\ast }}{4},F(y,x)=\frac{y-x}{4}$$

and $F(y^{\ast },x^{\ast })=0$. Therefore

$$\begin{array}{c}q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\hfill \\ =q(0,\frac{x^{\ast }-y^{\ast }}{4})+q(\frac{y-x}{4},0)\hfill \\ =\frac{1}{4}|0-(x^{\ast }-y^{\ast })|+\frac{1}{4}|y-x|+\frac{1}{4}(y-x)\hfill \\ =\frac{1}{4}(x^{\ast }-y^{\ast })+\frac{1}{4}(y-x)+\frac{1}{4}(y-x)\hfill \\ =\frac{1}{2}((\frac{1}{2}{x}^{\ast }-\frac{1}{2}x)-\frac{1}{2}x+(\frac{1}{2}y-\frac{1}{2}{y}^{\ast })+\frac{1}{2}y)\hfill \\ \le \frac{1}{2}((\frac{1}{2}{x}^{\ast }-\frac{1}{2}x)+\frac{1}{2}x+(\frac{1}{2}y-\frac{1}{2}{y}^{\ast })+\frac{1}{2}y)\hfill \\ \le \frac{1}{2}(|\frac{1}{2}{x}^{\ast }-\frac{1}{2}x|+\frac{1}{2}x+|\frac{1}{2}{y}^{\ast }-\frac{1}{2}y|+\frac{1}{2}y)\hfill \\ =\frac{1}{2}(|g{x}^{\ast }-gx|+gx+|gy-g{y}^{\ast }|+gy)\hfill \\ =\frac{1}{2}(q(gx,g{x}^{\ast })+q(gy,g{y}^{\ast })).\hfill \end{array}$$

Case 3: $x>y$ and $x^{\ast }<y^{\ast }$. Using similar arguments to those given in Case (2), we can show that

$$q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\le \frac{1}{2}(q(gx,g{x}^{\ast })+q(gy,g{y}^{\ast })).$$

Case 4: $x\ge y$ and $x^{\ast }\ge y^{\ast }$. Using similar arguments to those given in Case (1), we can show that

$$q(F(x,y),F(x^{\ast },y^{\ast }))+q(F(y,x),F(y^{\ast },x^{\ast }))\le \frac{1}{2}(q(gx,g{x}^{\ast })+q(gy,g{y}^{\ast })).$$

Thus F and g satisfy all the hypotheses of Corollary 2.7. So, F and g have a unique common fixed point. Here $(0,0)$ is the unique common fixed point of F and g. □

We end with an example related to Theorem 2.2.

Example 3.2 Let $X=[0,+\mathrm{\infty })$. Define

$$q:X\times X\to {\mathbb{R}}^{+},q(x,y)=|x-y|+x.$$

Also, define

$$\begin{array}{c}F:X\times X\to X,F(x,y)=x;g:X\to X,\hfill \\ gx=2x;\varphi :X\to {\mathbb{R}}^{+},\varphi (x)=2x.\hfill \end{array}$$

Then:

• (1) $(X,q)$ is a complete quasi-partial metric space.

• (2) $F(X\times X)\subseteq gX$.

• (3) For any $x,y\in X$, we have

  $$q(gx,F(x,y))+q(gy,F(y,x))\le \varphi (gx)+\varphi (gy)-\varphi (F(x,y))-\varphi (F(y,x)).$$

• (4) Let $G:X\times X\to {\mathbb{R}}^{+}$ be defined by $G(x,y)=q(F(x,y),gx)$. If $(g{x}_n)$ and $(g{y}_n)$ are two sequences in X with $(g{x}_n,g{y}_n)\to (u,v)$, then $G(u,v)\le 4{lim\hspace{0.17em}inf}_{n\to +\mathrm{\infty }}G(x_n,y_n)$.

Proof The proofs of (1) and (2) are clear. To prove (3) given $x,y\in X$, $gx=2x$, $gy=2y$, $F(x,y)=x$, $F(y,x)=y$, $\varphi (x)=2x$ and $\varphi (y)=2y$. Thus

$$\begin{array}{rcl}q(gx,F(x,y))+q(gy,F(y,x))& =& q(2x,x)+q(2y,y)\\ =& 2x+2y\\ \le & 4x+4y-2x-2y\\ =& \varphi (2x)+\varphi (2y)-\varphi (x)-\varphi (y)\\ =& \varphi (gx)+\varphi (gy)-\varphi (F(x,y))-\varphi (F(y,x)).\end{array}$$

To prove (4), let $(g{x}_n)$ and $(g{y}_n)$ be two sequences in X such that $(g{x}_n,g{y}_n)\to (u,v)$ for some $u,v\in X$. Then $g{x}_n\to u$ and $g{y}_n\to v$. Thus

$$q(g{x}_n,u)=q(2x_n,u)\to q(u,u)$$

and

$$q(u,g{x}_n)=q(u,2x_n)\to q(u,u).$$

Therefore

$$|2x_n-u|+2x_n\to u$$

and

$$|u-2x_n|+u\to u.$$

Therefore

$$|u-2x_n|\to 0.$$

Hence $x_n\to \frac{1}{2}u$ in ${\mathbb{R}}^{+}$. Now

$$\begin{array}{rcl}G(u,v)& =& q(F(u,v),u)\\ =& q(u,u)\\ =& u\\ \le & 4\left(\frac{1}{2}u\right)\\ =& 4\underset{n\to +\mathrm{\infty }}{lim\hspace{0.17em}inf}{x}_n\\ =& 4\underset{n\to +\mathrm{\infty }}{lim\hspace{0.17em}inf}G(x_n,x_n)\\ =& 4\underset{n\to +\mathrm{\infty }}{lim\hspace{0.17em}inf}G(F(x_n,y_n),x_n).\end{array}$$

So, F and g satisfy all the hypotheses of Theorem 2.2. Hence F and g have a coupled coincidence point. Here $(0,0)$ is the coupled coincidence point of F and g. □