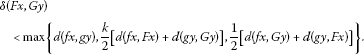- Research
- Open access
- Published:
Common fixed point theorems for two hybrid pairs of mappings satisfying the common property (E.A) in Menger PM-spaces
Fixed Point Theory and Applications volume 2013, Article number: 25 (2013)
Abstract
In this paper, a new concept of the common property (E.A) for two hybrid pairs of mappings is introduced in Menger PM-spaces. Utilizing this concept, some common fixed point theorems, which shed some new light on the study of fixed point results for hybrid pairs in Menger PM-spaces, are obtained under strict contractive conditions. The corresponding results in metric spaces which generalize many known results are also obtained. Finally, an example is also given to exemplify our main results.
1 Introduction
The concept of a probabilistic metric space was initiated and studied by Menger which is a generalization of the metric space notion [1, 2]. The theory of a probabilistic metric space is an active field and has applications in many other branches of mathematics such as cluster analysis, mathematical statistics and chaos theory [3, 4]. It has also been applied to quantum particle physics in connection with both string and theory [5].
Fixed point theory in a probabilistic metric space is an important branch of probabilistic analysis, which is closely related to the existence and uniqueness of solutions of differential equations and integral equations [6, 7]. Many results on the existence of fixed points or solutions of nonlinear equations under various types of conditions in Menger spaces have been extensively studied by many scholars (see, e.g., [8, 9]).
Jungck [10] introduced the concept of compatible mappings in metric spaces and proved some common fixed point theorems. In [11], the concept of weakly compatible mappings was given. The concept of compatible mappings in a Menger space was initiated by Mishra [12], and since then many fixed point results for compatible mappings and weakly compatible mappings have been studied [13–16]. The study for noncompatible mappings is also interesting. This was initiated and studied by Pant first in metric spaces [17–20]. In 2002, Aamri and Moutawakil defined a new property for a pair of mappings, i.e., the so-called property (E.A), which is a generalization of noncompatibility [21]. Using this property, some common fixed point theorems under strict contractive conditions in metric spaces have been given. In 2004, Kamran introduced the concept of the property (E.A) in a hybrid case in metric spaces and obtained some coincidence and fixed points theorems for hybrid strict contractions [22]. However, Sintunavarat and Kumam pointed out that one condition in one of their main results is superfluous [23]. Liu et al. defined the concept of the common property (E.A) for single-valued as well as hybrid pairs of mappings in metric spaces and obtained many interesting results [24]. Utilizing these concepts, many authors studied the existence of coincidence and fixed points in symmetric spaces [25–28].
On the other hand, fixed point results for mappings under strict contractive conditions in probabilistic metric spaces are not very fruitful. In 2009, Fang defined the property (E.A) for two single-valued mappings in Menger PM-spaces and studied the existence of common fixed points in such spaces [29]. In 2011, Ali et al. obtained some common fixed point results for strict contractions in Menger PM-spaces using the common property (E.A) for two pairs of single-valued mappings [30].
The purpose of this paper is to introduce the concept of the common property (E.A) for two hybrid pairs of mappings in Menger PM-spaces and study the existence of coincidence and common fixed points for pairs of mappings satisfying such a property under strict contractive conditions. We also obtain some corresponding results under strict contractive conditions in metric spaces.
2 Preliminaries
A mapping is called a distribution function if it is nondecreasing left-continuous with and .
We will denote by the set of all distribution functions, while H will always denote the specific distribution function defined by
Let . The algebraic sum is defined by
for all .
Let f and g be two functions defined on ℝ with positive values. The notation means that for all , and there exists at least one such that .
A mapping is called a triangular norm (for short, a t-norm) if the following conditions are satisfied:
-
(1)
;
-
(2)
;
-
(3)
for , ;
-
(4)
.
Definition 2.1 [4]
A triplet is called a Menger probabilistic metric space (for short, a Menger PM-space) if X is a nonempty set, Δ is a t-norm and ℱ is a mapping from into satisfying the following conditions (we denote by ):
(MS-1) for all if and only if ;
(MS-2) for all ;
(MS-3) for all and .
Remark 2.1 In [7], it is pointed out that if satisfies the condition , then is a Hausdorff topological space in the -topology , i.e., the family of sets () is a basis of neighborhoods of a point x for , where .
By virtue of this topology , a sequence is said to be -convergent to (we write ) if for any given and , there exists a positive integer such that whenever , which is equivalent to for all ; is called a -Cauchy sequence in if for any given and , there exists a positive integer such that whenever ; is said to be -complete if each -Cauchy sequence in X is -convergent in X. Note that in a Menger PM-space, when we write , it means that .
Let be a PM-space and A be a nonempty subset of X. Then the function
is called the probabilistic diameter of A. If , then A is said to be probabilistically bounded.
Let be a metric space, be the family of all nonempty bounded closed subsets of X and δ be the Hausdorff metric induced by d, that is,
for any , where .
Let be a Menger space and Ω be the family of all nonempty probabilistically bounded -closed subsets of X. For any , define the distribution functions as follows:

where is called the Menger-Hausdorff metric induced by ℱ.
Remark 2.2 [7]
-
(1)
is a metric space. If is complete, then is complete.
-
(2)
Let be a metric space. Define a mapping by
Then is a Menger PM-space induced by with , . If is complete, then is -complete.
-
(3)
If we define as follows:
then is the Menger-Hausdorff metric induced by ℱ. Moreover, if is a -complete Menger PM-space with the t-norm , where , , then is also a -complete Menger PM-space.
The following lemmas play an important role in proving our main results in Section 3.
Lemma 2.1 [7]
Let be a Menger PM-space. Then for any and any , we have the following:
-
(i)
if and only if ;
-
(ii)
if and only if ;
-
(iii)
For any , for all ;
-
(iv)
for all ;
-
(v)
for all ;
-
(vi)
for all .
Lemma 2.2 [7]
Let be a Menger PM-space with a continuous t-norm Δ on , , and , . Then for all . Particularly, if is continuous at the point , then .
Imitating the proof of Lemma 2.2 and using Lemma 2.1, we can easily obtain the following two lemmas.
Lemma 2.3 Let be a Menger PM-space with a continuous t-norm Δ on and be the induced Menger PM-space, , , , and , . Then for all . Particularly, if is continuous at the point , then .
Lemma 2.4 Let be a Menger PM-space with a continuous t-norm Δ on and be the induced Menger PM-space, , and , . Then for all . Particularly, if is continuous at the point , then .
We recall the definition of compatibility in a hybrid case and weakly compatibility in both single-valued and hybrid case in Menger PM-spaces.
Definition 2.2 [15]
Let be a Menger PM-space and be the induced Menger PM-space. Then and are said to be compatible if for all and for all whenever is a sequence in X such that and .
Definition 2.3 [13]
Let be a Menger PM-space. Then and are said to be weakly compatible if they commute at their coincidence points, i.e., whenever .
Definition 2.4 [15]
Let be a Menger PM-space, be the induced Menger PM-space. Then and are said to be weakly compatible if they commute at their coincidence points, i.e., whenever .
In the sequel, we will denote by the set of all coincidence points of f and F.
We first give the definition of the property (E.A) for a hybrid pair of mappings in Menger PM-spaces.
Definition 2.5 Let be a Menger PM-space, be the induced Menger PM-space, be a self-mapping and be a multivalued mapping. A pair of mappings is said to satisfy the property (E.A) if there exists a sequence in X and some and such that .
Remark 2.3 Similar to the arguments in [29], by this definition, we can also see that in a hybrid case, any noncompatible mappings satisfy the property (E.A). But the following example shows that the converse is not true.
Example 2.1 Let . Define and as follows:

Then by Remark 2.2, we know that and are both Menger PM-spaces. Define and as and take . Then , , which implies that , and so satisfies the property (E.A). On the other hand, suppose that is an arbitrary sequence in X satisfying for some and . Then , which implies that for all . So, f and F are compatible mappings.
We now give the definition of the common property (E.A) for two hybrid pairs of mappings in Menger PM-spaces.
Definition 2.6 Let be a Menger PM-space and be the induced Menger PM-space, and . Two pairs of mappings and are said to satisfy the common property (E.A) if there exist two sequences , in X and some and such that
Example 2.2 Let be a metric space, , and be two Menger PM-spaces induced by and , respectively (as in Remark 2.2). Define and as follows:
Consider the sequence , and denote , .
Since , while (), we have , , i.e., . Similarly, we have , , i.e., .
On the other hand, since , while (), we have , , i.e., as . Similarly, we have , , i.e., as . Thus, the pairs of mappings and satisfy the common property (E.A).
3 Main results
In this section, we will give the main results of this paper. We first present the following common fixed point theorem for two hybrid pairs of mappings in Menger PM-spaces.
Theorem 3.1 Let be a Menger PM-space with Δ a continuous t-norm on and be the induced Menger PM-space. Suppose that and are mappings satisfying the following conditions:
-
(i)
and satisfy the common property (E.A);
-
(ii)
and are -closed subsets of X;
-
(iii)
For any with and some ,
(3.1)
where means . Then and each has a coincidence point. Moreover, if for and for , then f, g, F and G have a common fixed point in X.
Proof Since and satisfy the common property (E.A), there exist and some , such that
Since is -closed, there exists some such that . We claim that . Suppose this is not true, that is, . Then from , we have . Thus, there exists some such that
(Otherwise, , as , that is, , , which is a contradiction.)
Without loss of generality, we can assume that is a continuous point of . In fact, by the left continuity of the distribution function, we know that there exists some such that
Since the distribution function is nondecreasing, the discontinuous points are at most a countable set. Thus, when is not a continuous point of , we can always choose a point in to replace .
Noting that and , we have , so there exists some such that for all , .
From (3.1) we know that

It is easy to verify that
In fact, for any , we have
Since , by Lemma 2.3 and Lemma 2.1(ii), we get
Letting , by the left continuity of the distribution function, we obtain (3.5). Similarly, we can prove that
Noting that is the continuous point of , by Lemma 2.4, we have
Thus, letting in (3.4) and using (3.5) and (3.6), we obtain
that is,
But since , by Lemma 2.1(iii), (3.3) implies that
which is a contradiction. So, we get .
On the other hand, since is -closed, there exists some such that . We claim that . Suppose this is not true, that is, . Noting that , we have . Similarly, we know that there exists some such that
Similarly, without loss of generality, we can assume that is a continuous point of .
Noting that and , we have , so there exists some such that for all , .
From (3.1) we know that

It is easy to verify that
In fact, for any , we have
Since , by Lemma 2.3 and Lemma 2.1(ii), we get
Letting , by the left continuity of the distribution function, we obtain (3.9). Similarly, we can prove that
Noting that is the continuous point of , by Lemma 2.4, we have
Thus, letting in (3.8) and using (3.9) and (3.10), we obtain
that is,
But since , by Lemma 2.1(iii), (3.7) implies that
which is a contradiction. So, we get . Therefore, we have proved , and , i.e., v is a coincidence point of and w is a coincidence point of .
Since and , we have and . Next, we prove that and .
First, we assert that . In fact, suppose that . Then by (3.1), there exists some such that
This implies that
which is a contradiction, and thus we have .
Similarly, we can prove that . In fact, suppose that . Then by (3.1), there exists some such that
This implies that
which is a contradiction, and thus we have . Combining these two facts yields .
Next, we assert that . Suppose that . Again by (3.1), there exists some such that
This implies that
which is a contradiction, and so we have . Combining this with , we obtain .
Thus, we have and , that is, u is the common fixed point of f, g, F and G. This completes the proof. □
From the proof of Theorem 3.1, we can similarly prove the following result.
Theorem 3.2 Let be a Menger PM-space with Δ a continuous t-norm on and let be the induced Menger PM-space. Suppose that and are mappings satisfying the conditions (i)-(ii) of Theorem 3.1 and the following:
(iii)′ For any with and some ,
where means . Then and each has a coincidence point. Moreover, if for and for , then f, g, F and G have a common fixed point in X.
Setting in Theorem 3.1, we obtain the following corollary.
Corollary 3.1 Let be a Menger space with Δ a continuous t-norm on and let be the induced Menger space. Suppose that and are mappings satisfying the following conditions:
-
(i)
and satisfy the common property (E.A);
-
(ii)
is a -closed subset of X;
-
(iii)
For any with and some ,
(3.12)
where means . Then f, F and G have a coincidence point. Moreover, if for and , then f, F and G have a common fixed point in X.
Setting and , we have the following corollary.
Corollary 3.2 Let be a Menger space with Δ a continuous t-norm on and let be the induced Menger space. Suppose that and are mappings satisfying the following conditions:
-
(i)
satisfies the property (E.A);
-
(ii)
is a -closed subset of X;
-
(iii)
For any with and some ,
(3.13)
where means . Then f and F have a coincidence point. Moreover, if for , then f and F have a common fixed point in X.
If f, g, F and G are all single-valued mappings, then we have the following corollary.
Corollary 3.3 Let be a Menger space with Δ a continuous t-norm on . Suppose that are self-mappings satisfying the following conditions:
-
(i)
and satisfy the common property (E.A);
-
(ii)
and are -closed subsets of X;
-
(iii)
For any with and some ,
(3.14)
where means . Then and each has a coincidence point. Moreover, if for and for , then f, g, F and G have a common fixed point in X.
Remark 3.1 We would like to point out here that in the condition (iii), we use ‘for any with ’ instead of ‘for any with ’ as in Theorem 2.1 of [30] when we consider two pairs of mappings. Moreover, comparing our Corollary 3.3 with Theorem 2.1 of [30], one can find that we use the condition ‘ for and for ’ instead of weakly compatibility condition for two hybrid pairs. In fact, in a hybrid case, even if and are weakly compatible, we still cannot obtain the conclusion.
Remark 3.2 Similarly, some other corresponding corollaries can be obtained from Theorem 3.2. For simplicity, we omit them here. Also, it is worth mentioning that in all of the above theorems and corollaries, we do not need any condition on the continuity or the containment of the ranges of involved mappings.
4 Common fixed point results in metric spaces
In this section, we use the results in Section 3 to get some corresponding results in metric spaces.
Theorem 4.1 Let be a metric space. Suppose that and are mappings satisfying the following conditions:
-
(i)
and satisfy the common property (E.A);
-
(ii)
and are closed subsets of X;
-
(iii)
For any with and some ,
 (4.1)
(4.1)
Then and each has a coincidence point. Moreover, if for and for , then f, g, F and G have a common fixed point in X.
Proof Let be the induced Menger space by and be the induced Menger space by . Then by Remark 2.2, it is easy to see that Theorem 4.1(i) and (ii) imply Theorem 3.1(i) and (ii). Now we show that Theorem 4.1(iii) implies Theorem 3.1(iii).
We first verify that for any with and , the following holds:
If , then , and thus (4.2) obviously holds.
If , we consider the following three cases:
Case (I): . In this case, , and thus (4.2) holds.
Case (II): , that is, . Then for any with , we have or , which implies that or . Hence,
and so (4.2) holds.
Case (III): . Similar to Case (II), we can prove that , so (4.2) holds.
From the above discussions, we conclude that (4.2) is always true.
Next, by (4.1), there exists some such that
This implies that and
which yields that
Combining (4.2) with (4.3), we know that (3.1) holds. □
Similarly, from Theorem 3.2, we can obtain the following theorem.
Theorem 4.2 Let be a metric space. Suppose that and are mappings satisfying the following conditions:
-
(i)
and satisfy the common property (E.A);
-
(ii)
and are closed subsets of X;
-
(iii)
For any with and some ,
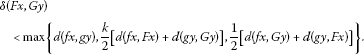 (4.4)
(4.4)
Then and each has a coincidence point. Moreover, if for and for , then f, g, F and G have a common fixed point in X.
Remark 4.1 Note that when , then (4.4) becomes (2.3) in Theorem 2.3 of [24]. Similar to Remark 3.1, we should state ‘for any with ’ here instead of ‘for any with ’ as in [24]. Moreover, we only need ‘ for and for ’ to guarantee the existence of common fixed points of f, g, F and G. In fact, the condition ‘f is F-weakly commuting for and g is G-weakly commuting for ’ is superfluous in Theorem 2.3 of [24].
Remark 4.2 By Corollary 3.1-Corollary 3.3 and Remark 3.2, we can also obtain some other corresponding corollaries for common fixed point theorems in metric spaces, which are the generalizations of many known results (e.g., [22, 23]). For the sake of simplicity, we omit them here.
5 An application
In this section, we will provide an example to exemplify the validity of the main result of this paper.
Example 5.1 Consider and define for all with . Also, let be the family of nonempty bounded closed subsets of X and define for all with . Then and are both Menger PM-spaces with , where Ω is the family of all nonempty probabilistically bounded -closed subsets of X. Define and as follows:

Consider the sequences and in X, then
which shows that and satisfy the common property (E.A). Also, and are -closed subsets of X. By a routine calculation, one can verify the inequality (3.1) for any with and some .
In fact, if and , then for , we have
If and , then for , we have
Similarly, it is easy to verify (3.1) for other cases. Thus, all the conditions of Theorem 3.1 are satisfied and 0 is the unique coincidence point of and . Furthermore, noting that and , 0 remains the common fixed point of and .
It is worth pointing out that many theorems in some corresponding published papers cannot be applied to this example since Theorem 3.1 does not require any condition on the containment of the ranges of involved mappings, and in this example we also do not require such containment.
References
Menger K: Statistical metrics. Proc. Natl. Acad. Sci. USA 1942, 28: 535–537. 10.1073/pnas.28.12.535
Schweizer B, Sklar A: Statistical metric spaces. Pac. J. Math. 1960, 10: 313–334. 10.2140/pjm.1960.10.313
Schweizer B, et al.: Commentary on probabilistic geometry. 2. In Karl Menger, Selecta Mathematica. Edited by: Schweizer B, Sklar A, Sigmund K. Springer, New York; 2003:409–432.
Schweizer B, Sklar A: Probabilistic Metric Spaces. North-Holland, Amsterdam; 1983.
El Naschie MS: A review of applications and results of E-infinity theory. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8: 11–20.
Hadz̆ić O, Pap E: Fixed Point Theory in Probabilistic Metric Spaces. Kluwer Academic, Dordrecht; 2001.
Chang SS, Cho YJ, Kang SM: Nonlinear Operator Theory in Probabilistic Metric Spaces. Nova Science Publishers, New York; 2001.
Zhu CX: Several nonlinear operator problems in the Menger PN space. Nonlinear Anal. 2006, 65: 1281–1284. 10.1016/j.na.2005.10.019
Zhu CX: Research on some problems for nonlinear operators. Nonlinear Anal. 2009, 71: 4568–4571. 10.1016/j.na.2009.03.014
Jungck G: Compatible mappings and common fixed points. Int. J. Math. Math. Sci. 1986, 9: 771–779. 10.1155/S0161171286000935
Jungck G: Common fixed points for non continuous non self maps on non metric spaces. Far East J. Math. Sci. 1996, 4: 199–215.
Mishra SN: Commond fixed points of compatible mappings in PM-spaces. Math. Jpn. 1991, 36: 436–440.
Singh B, Jain S: A fixed point theorem in Menger space through weak compatibility. J. Math. Anal. Appl. 2005, 301: 439–448. 10.1016/j.jmaa.2004.07.036
Razani A, Shirdaryazdi M: A common fixed point theorem of compatible maps in Menger space. Chaos Solitons Fractals 2007, 32: 26–34. 10.1016/j.chaos.2005.10.096
Wu ZQ, Zhu CX, Chen XL: Fixed point theorems and coincidence point theorems for hybrid contractions in PM-spaces. Acta Anal. Funct. Appl. 2008, 10(4):339–345. (in Chinese)
Fang JX: Common fixed point theorems of compatible and weakly compatible maps in Menger spaces. Nonlinear Anal. 2009, 71: 1833–1843. 10.1016/j.na.2009.01.018
Pant RP: Common fixed points of contractive maps. J. Math. Anal. Appl. 1998, 226: 251–258. 10.1006/jmaa.1998.6029
Pant RP: R-weakly commutativity and common fixed points. Soochow J. Math. 1999, 25: 37–42.
Pant RP, Pant V: Common fixed under strict contractive conditions. J. Math. Anal. Appl. 2000, 248: 327–332. 10.1006/jmaa.2000.6871
Pant RP, Pant V, Jha K: Note on common fixed points under strict contractive conditions. J. Math. Anal. Appl. 2002, 274: 879–880. 10.1016/S0022-247X(02)00309-8
Aamri M, El Moutawakil D: Some new common fixed point theorems under strict contractive conditions. J. Math. Anal. Appl. 2002, 270: 181–188. 10.1016/S0022-247X(02)00059-8
Kamran T: Coincidence and fixed points for hybrid strict contractions. J. Math. Anal. Appl. 2004, 299: 235–241. 10.1016/j.jmaa.2004.06.047
Sintunavarat W, Kumam P: Coincidence and common fixed points for hybrid strict contraction without the weakly commuting condition. Appl. Math. Lett. 2009, 22: 1877–1881. 10.1016/j.aml.2009.07.015
Liu YC, Wu J, Li ZX: Common fixed points of single-valued and multivalued maps. Int. J. Math. Math. Sci. 2005, 19: 3045–3055.
Imdad M, Ali J, Khan L: Coincidence and fixed points in symmetric spaces under strict contractions. J. Math. Anal. Appl. 2006, 320: 352–360. 10.1016/j.jmaa.2005.07.004
Imdad M, Ali J, Khan L: Corrigendum to ‘Coincidence and fixed points in symmetric spaces under strict contractions’ [J. Math. Anal. Appl. 320 (2006) 352–360]. J. Math. Anal. Appl. 2007, 329: 752. 10.1016/j.jmaa.2006.06.057
Aliouche A: A common fixed point theorem for weakly compatible mappings in symmetric spaces satisfying a contractive condition of integral type. J. Math. Anal. Appl. 2006, 322: 796–802. 10.1016/j.jmaa.2005.09.068
Djoudi A, Aliouche A: Common fixed point theorems of Gregus type for weakly compatible mappings satisfying contractive conditions of integral type. J. Math. Anal. Appl. 2007, 329: 31–45. 10.1016/j.jmaa.2006.06.037
Fang JX, Gang Y: Common fixed point theorems under strict contractive conditions in Menger spaces. Nonlinear Anal. 2009, 70: 184–193. 10.1016/j.na.2007.11.045
Ali J, Imdad M, Mihet D, Tanveer M: Common fixed points of strict contractions in Menger spaces. Acta Math. Hung. 2011, 132(4):367–386. 10.1007/s10474-011-0105-3
Acknowledgements
The authors would like to thank the editor and the referees for their constructive comments and suggestions. The research was supported by the Natural Science Foundation of China (11071108), the Natural Science Foundation of Jiangxi Province of China (2010GZS0147, 20114BAB201003), and partly supported by the Humanities and Social Sciences Foundation of Ministry of Education of China (12YJC630091) and the Natural Science Foundation of Zhejiang Province of China (LQ12G02007).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu, Z., Zhu, C. & Li, J. Common fixed point theorems for two hybrid pairs of mappings satisfying the common property (E.A) in Menger PM-spaces. Fixed Point Theory Appl 2013, 25 (2013). https://doi.org/10.1186/1687-1812-2013-25
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2013-25